사라진 블로그! 연락 주시면 새로운 블로그 알려드립니다 ~

시험이 끝나고 까먹지 말자고 적는 글이..지만 이번 단원은 쉬어가기 단원이라 생각할 정도로 내용이 없어요. 와ㅏㅏ

무엇을 배웠을까 (15.1~15.8)

이중적분 하는 법 / 변수 순서 바꾸기 / 극좌표로 변환하기
삼중적분 하는 법 / 변수 순서 바꾸기 / 실린더 모양 극좌표로 변환하기 ($(x,y,z)\rightarrow \ (r,\theta,z)$ 자코비안은 $r$) / 구 모양 극좌표로 변환하기 ($(x,y,z)\rightarrow \ (\rho,\theta,\phi)$ 자코비안은 $\rho^2 sin\phi$)


여기까지는 고딩 때 물리2 했다면 회전관성이나 전자기장 세기 같은 거 구하면서 야매로 쓰던 개념을 체계적으로 잡아주는 느낌이었어요.

자코비안이라는 새로운 용어가 보이는데 이는 15.9절부터 정식으로 등장합니다!
15.8절까지는 그냥 "저렇게 좌표 변환 하면 이걸 추가로 곱해줘야 해" 식으로 배우죠 ㅎㅎ (물론 증명하고)

물2 했으면 새로 배우는 내용 (15.9)

$(x,y,z)$를 $(r,\theta,z)$나 $(\rho,\theta,\phi)$ 로 바꾸는 건 먼가 특수한 경우죠. 여기서부터는 이를 일반화시키는 내용을 배웁니다.

다시 실린더모양 극좌표 변환 부분을 이해해보면
$D=\{(x,y)\mid 1\leq x^2+y^2\leq4 \}$
이를 적분하기 위해서는 x와 y가 종속되어 있어서 푸비니 정리도 사용하지 못하고 상당히 더럽죠. 우엥

그래서 $(r,\theta)$ 좌표로 바꿔주면
$D=\{(r,\theta)\mid 1\leq r \leq 2, 0 \leq \theta \leq 2\pi \}$
이를 그래프로 보면 좀 와닿는데요.

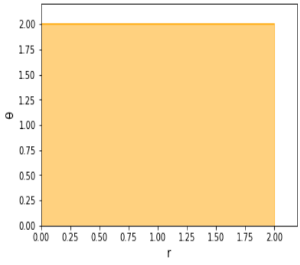
원래 원형이었던 $r$과 $\theta$가 직사각형이 되었어요. 와, 적분이 깨알만큼 쉬워졌죠!!
이처럼 Domain의 형태를 원하는 대로 바꿀 수 있는데, 15.7~8에서는 Cylindrical Coordinate과 Spherical Coordinate만 취급했다면 15.9는 일반화되어 이것저것 합니다.

즉, 15.9에서 배우는 변환의 핵심은 4개의 함수로 bounded된 2차원 도형에서, 둘 둘 모양이 비슷하면 이를 상수취급해서 네모형태로 바꾸어 적분을 쉽게(?) 하는 것입니다. 예제는 나중에 추가할게요

Domain만 바꿨다고 적분 끝난게 아니고, 적분인자 앞에 무언가가 곱해지는데, 이를 자코비언이라고 합니다.
이것도 인터넷 검색하면 나오는데 나중에 추가할래요.

근데 내용 진짜 저거 두개긴 해요. $(x,y)$를 $(u,v)$로 바꾸기 위한 변환을 구하고, 자코비언 구하고, 적분하면 끝!

내용은 쉬워보이지만 적분은 쉽지 않기에 시험은 또 망했어요ㅠㅠ
교재의 연습문제도 그렇구 배우는 내용은 어떻게 하면 다중적분을 더 쉽게 할까인 것 같은데, 정작 시험으로 주는 문제는 온갖 꼼수를 써도 계산량 엄청난 것들,,

제목이 거창한데 사실 네모가 미적공부하며 헷갈린 것입니다ㅎㅅㅎ
저는 미적 뉴비이기 때문에 오개념 지적은 감사히 받습니다.

$\vec{r''(t)}$과 $\vec{N(t)}$의 방향이 같지 않을까?

엄청난 미분과 제곱과 루트 연산에 지치다보면 저런 생각을 할 수도 있습니다. 그렇지만 슬프게도 아님니다 ㅠㅠ 다름니다.

$\vec{N(t)}=\frac{\vec{T'(t)}}{\left | \vec{T'(t)} \right |}$
저기 절댓값 들어간 분모가 t 로 표현되었죠 ㅎㅅㅎ.. 저걸 없애고 미분하면 결과가 달라지겠죠?

사실 좀더 생각해보면
$\vec{r''(t)}$은 $\vec{r'(t)}$의 변화량 같은 거라 $\vec{T}$에 수직함이 보장되지 않음이 자명하죠..아ㅠㅠ 계산 시러

Gradient가 대체 먼가요?

아래의 영상이 매우 친절하게 설명해줍니다. 저 같은 미알못의 하찮은 질문을 받아주시는 분이 추천한 영상인데, 영어로 되어있지만 귀에 잘 들어옵니다. 개념 정립도 잘되구요 ㅎㅅㅎ
https://www.youtube.com/watch?v=GkB4vW16QHI&feature=share
좀 더 알아둘만한 거 한 가지 적자면
그래디언트가 언덕 위에 있는 건지 아니면 z축 성분이 없는 지 책에 나오는 그림을 아무리 봐도 좀 헷갈리는데 (영어를 못해서)
그래디언트는 원래 함수보다 차원이 하나 떨어진다.. 정도? 후자가 맞습니다.

끼적.. 사실 저도 잘 몰라요.

Lagrange Multiplier Method으로 Min/Max 구하기

까먹지 말자고 끄트머리에 써봅니당 ㅎ 이름이 매우 간지나지만, 사실 고딩 때 하던 것의 다차원 버전입니다. 그런데 전 고딩 때 수학을 던졌죠 젠장;;
사실 전 앞에서부터 개념 흔들려서, 막판엔 그냥 기출을 쌩으로 외워서 좀 오개념이 있을 수도 있습니다.

[1단계] 1) 편미분해서 0이나 무한이 되거나, 2) boundary인 지점을 조사합니다.
이 때
[2단계] 1)에서 구한 critical point 중 임계점을 찾아 제낍니다. 이 때 임계점을 찾는 방법은 정의를 이용할 수도 있으나, 판별식(

)를 이용하는 것이 일반적인 듯합니다.
D>0이면 극값이 존재하는데 Fxx가 양수면 Local min, 음수면 Local max입니다.

마지막으로 쭉 비교해주며 absol min/max를 찾던 후처리해주면 됩니다.

대강 생각나는 건 이정도...? 몇 개 모두가 아는 미적분학 시험기간 벼락치기 꿀팁 더 쓰자면

13.1~13.3은 공식 암기와 계산입니다. 딱히 꼬아서 안 내는 것 같으니 r,T,N,B,카파,로 이런 친구들간 관계된 식 다 외우고, 이악물고 계산하면 되는 것 같습니다.
===============================================
T와 N으로 만들어지는 osculating plane(접촉평면, 즉 곡선이 누워있는 평면)의 normal vector는 B 이고
B와 N으로 만들어지는 normal plane(곡선이 수직으로 뚫는 평면)의 normal vector는 T // r'입니다.
=================================================
14절 초반에 Continuity 증명할 때 절대부등식 몇 개 알고 있으면 입델 없이도 Squeeze Thm으로 간단히 끝낼 수 있습니다.
산술기하, 코시 슈바르츠 이런 친구들은 고등 교육과정에서 나오니 어느 정도 자유자재로 쓸 정도로는 알아둡시다. sinx, tanx 나오면 x로 막고, 이상한 수들이 제곱되어 더해져 있으면 절대부등식 한 번 써봅니다.
===================================================
Duf (아직도 얘를 어떻게 읽는지 모릅니다ㅎ;)란 친구의 전방향 존재성 보일 때는 정의로 접근함시당. fx랑 fy 쓰는 방법은 미분가능성이 증명되었을 때만 쓸 수 있습니다. 그래서 틀렸음
================================================
빨리 계절미적이 좀 끝나길 바라며 >__<